2.1 원자 이론의 역사적 발전
2.1.1 주기율표
2.1.2 원자구성 입자(Subatomic Particles)의 발견과 Bohr 원자
2.2 Schrodinger 방정식
2.2.1 상자 속 입자(Particle in a Box)
2.2.2 양자수와 원자 파동함수
2.2.3 쌓음 원리
2.2.4 가려막기
2.3 원자의 주기적 성질
2.3.1 이온화 에너지
2.3.2 전자 친화도
2.3.3. 공유 반지름과 이온 반지름
2.2 Schrodinger 방정식(1)
- 1926년과 1927년 Schrödinger와 Heisenberg는 매우 다른 수학적 기법을 사용한 파동역학(원자 내 전자의 파동 성질 설명)에 관한 논문 각각 발표
- 서로 다른 접근법을 사용하였음에도 불구하고 그들의 이론이 서로 같았음
- Schrödinger 방정식 : 전자의 파동성을 위치, 질량, 전체 에너지 및 퍼텐셜 에너지의 항으로 설명
- 방정식은 파동함수 ψ에 기초, 공간에서의 전자 파동을 나타냄(원자 궤도함수)

- H = 해밀턴 연산자
- E = 전자의 에너지
- ψ = 파동함수
- 해밀턴 연산자(Hamiltonian operator) : 파동함수를 연산하는 미분함수 포함
- 연산은 원자 궤도함수를 나타내는 어느 파동함수에 대해서도 이루어질 수 있음
- 서로 다른 궤도함수는 서로 다른 ψ 함수와 서로 다른 에너지 값 E를 가짐
- 이는 고유 함수 ψ로 특징되는 각각의 궤도함수가 특징적인 에너지를 갖는다는 양자화 설명하는 방법
- 에너지 준위를 계산할 때 쓰이는 형태로서 전자 하나의 시스템에 대한 해밀턴 연산자

- 왼쪽 : 전자의 운동 에너지를 나타냄
- 오른쪽 : 전자와 핵 사이에서 작용하는 정전기적인 인력의 결과로서 퍼텐셜 에너지를 나타내며, 일반적으로 V로 표시
- h = Plank 상수
- m = 입자(전자)의 질량
- e = 전자의 전하
- route(x2+y2+z2) = r = 핵으로부터의 거리
- Z = 핵의 전하
- 4πε0 = 진공에서의 유전율
이 연산자를 파동함수 ψ에 적용,


- 퍼텐셜 에너지 V : 전자와 핵 사이의 정전기적인 인력의 결과
- 양으로 하전된 핵과 음으로 하전된 전자 사이에서처럼 인력은 관습상 음의 퍼텐셜 에너지를 가진 것으로 정의
- 핵 근처에 가까이(작은 r 값) 있는 전자는 핵에 강하게 끌리고, 큰 음의 퍼텐셜 에너지를 가짐
- 핵에서 멀리 떨어진 전자는 작은 음의 퍼텐셜 에너지를 가짐
- 핵으로부터 무한정 멀리(r = ∞ ) 떨어진 전자는 원자핵과 전자 사이의 인력이 0이고, 퍼텐셜 에너지도 0임
- n은 1부터 ∞ 까지 가능하기 때문에 각각의 원자 궤도함수에 대해 고유한 ψ로 기술 가능
→ 원자에 대한 Schrödinger 방정식 해의 수는 제한이 없음
- 각각의 ψ는 특정한 궤도함수에서 주어진 전자의 파동성을 설명해 줌
- 공간상의 특정한 지점에서 전자를 발견할 확률은 ψ2에 비례
- ψ 가 물리적으로 가능한 값이 되기 위해 몇 가지 조건이 필요
1. 파동함수 ψ는 하나의 값(single-valued)을 가져야 함
: 공간상의 어느 지점에서 전자를 발견할 확률이 둘일 수 없음
2. 파동함수 ψ와 이의 일차 미분함수는 연속이어야 함
: 확률은 공간상의 모든 지점에 대하여 정의되어야 하고, 갑자기 한 곳에서 다른 곳으로 변할 수 없음
3. 파동함수 ψ는 r 값이 무한대에 접근함에 따라 0에 접근해야 함
: 핵으로부터 먼 거리에서의 확률은 점점 더 작아져야 함(원자는 유한해야 함)
4. 적분값

: 공간상의 어느 곳에서 전자를 발견할 전체 확률은 1임
- 이를 파동함수의 정규화(normalizing)라 함
5. 적분값

- ψA와 ψB는 같은 원자에서 전자의 다른 궤도함수를 나타냄
- 원자 내 모든 궤도함수는 서로 직교함
- px, py, pz에서처럼 궤도함수가 수직이어야 함을 의미
2.2.1 상자 속 입자(Particle in a Box)
- 간단한 파동방정식의 한 가지 예 : 일차원 상자 속 입자

- 상자 내인 x = 0부터 x = a 사이에서 퍼텐셜 에너지는 0으로 정의
- 상자 바깥쪽에서는 퍼텐셜 에너지가 무한대
- 이는 입자가 상자 속에 완전히 갇혀 있으며, 상자를 떠나려면 무한대의 에너지가 필요함을 의미
- 그러나 상자 낸에서 입자에 작용하는 힘은 없음
- 상자 내에서 위치에 대한 파동방정식
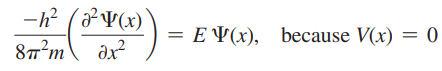
- 사인과 코사인 함수는 파동성(파장과 진폭으로 정의되는)을 갖고 있으며, 입자의 파동적 특징은 사인 및 코사인 함수의 조합으로 나타낼 수 있음
- 상자 속에서 가능한 파동을 표현하는 일반 해는 다음과 같음
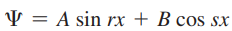
- A, B, r, s : 상수
- 파동방정식에 대입하면, r과 s에 대한 해를 얻을 수 있음
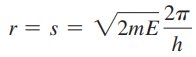
- ψ가 연속이어야 하고 x < 0과 x > a에서 0이어야 하므로(입자가 상자 속에 갇혀 있으므로), ψ는 x = 0과 x = a에서 0으로 가야 함
- x = 0에서 cos sx = 1이므로 ψ는 위의 일반 해에서 오직 B = 0인 경우에 0이 됨
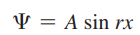
- x = a에서 ψ 또한 0이 되어야 함
- sin ra = 0이며, ra가 오직 π의 정수배인 경우에만 가능
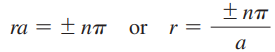
- 여기서 n = 정수 ≠ 0임
- 양의 r 값을 해에 치환하면 다음과 같음
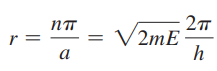
- 이 표현을 E에 대해서 풀기
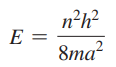
- 길이가 a인 일차원 상자 속 입자에 대한 모형으로부터 예측한 에너지 준위
- 에너지 준위는 양자수(quantum number) n = 1, 2, 3 · · ·로 양자화 되어 있음
- r = n π/a를 파동함수에 대입
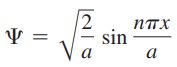
- 정규화 조건인
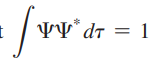
적용,
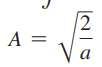
- 전체 해는 다음과 같음
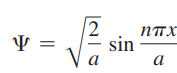
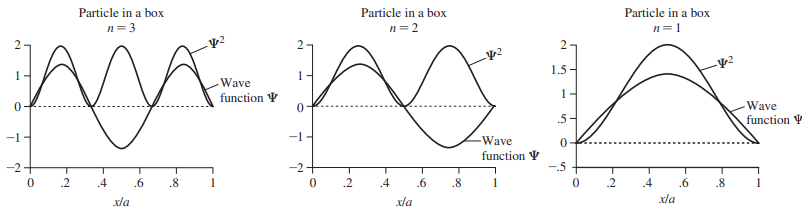
- 처음 세 가지 상태에 대한 파동함수와 이들의 제곱(바닥 상태와 2개의 들뜬 상태) 나타냄
- 파동함수의 제곱은 확률 밀도
- 상자 속 전자의 속성에 대한 고전역학과 양자역학의 차이점을 보여줌
- 고전역학 : 상자 내 어디서나 전자가 동일한 확률을 갖고있음을 예측
- 전자의 파동 성질 : 상자 속의 위치에 따라 전자가 발견될 확률이 달라짐
- ψ에 의해 정의되는 양자화된 에너지는 전자의 파동 진폭 제곱 값이 클수록 특정한 좌표에서 전자가 발견될 확률이 높음
Keyword: 해밀턴 연산자(Hamiltonian operator), 정규화(normalizing), 양자수(quantum number)



