2.1 원자 이론의 역사적 발전
2.1.1 주기율표
2.1.2 원자구성 입자(Subatomic Particles)의 발견과 Bohr 원자
2.2 Schrodinger 방정식
2.2.1 상자 속 입자(Particle in a Box)
2.2.2 양자수와 원자 파동함수
2.2.3 쌓음 원리
2.2.4 가려막기
2.3 원자의 주기적 성질
2.3.1 이온화 에너지
2.3.2 전자 친화도
2.3.3. 공유 반지름과 이온 반지름
2.1 원자 이론의 역사적 발전
원자 구조
- 양자역학이라는 정교한 수학보다 어느 정도의 수학적 지식만 가지고도 원자와 분자의 구조를 이해하는 것이 가능해짐
- 정성적인 또는 반정량적인(semiquantitative) 용어를 이용하여 원자와 분자 구조를 설명할 것
2.1 원자 이론의 역사적 발전
Democritus, Epicurus
- 원자의 본질에 관한 견해 제시
- 그럴듯한 원자 이론에 대해 필요한 정량적 상관관계가 실험을 통해 정립되는 데 수백 년이 걸림
John Dalton
- 원자는 간단한 정수비로 결합하여 화합물을 형성한다고 주장
- '모든 균일한 물체의 궁극적인 입자는 무게, 모양 등이 정확히 같다. 물 개개 입자는 다른 물의 입자와 동일하고, 모든 수소 입자는 다르수소 입자와 동일하다.'
- 원자나 분자 개념 분명히 제시
- 새로운 물질 형성 시 결합하는 물질의 부피와 질량에 관해 정량적으로 관찰
- '수소 두 분량과 산소 한 분량을 섞고 전기 방전을 이용하여 불을 붙이면 모두 수증기로 바뀌며, 압력이 충분히 높으면 수중기는 물로 변한다. 두 분량 수소의 입자수는 한 분량 산소 속의 입자수와 동일할 것'
- H2나 O2와 같은 이원자 분자를 H나 O와 같은 단원자라고 가정하여 물에 대한 정확한 화학식 발견 못함
- 기체 상태로 측정된 입자수에 대한 추측 화학식 2H2 + O2 → 2H2O와 현대의 개념인 몰(mole)비가 일치하지 않음
Avogardro
- 동일한 부피의 기체는 같은 온도와 압력에서 동일한 수의 분자를 갖고있음을 주장
- Gay-Lussac 자료 이용, 황, 인, 비소, 수은 증기의 성질에 대한 불확실성으로 개념 받아들이는 것이 늦어짐
+ 원자량과 분자식에 대한 광범위한 혼동
Kekule
- 아세트산에 대해 19가지의 서로 다른 가능한 구조 제시
Cannizzaro
- Avogardro의 주장 다시 발표
- 동일한 체계의 원자량을 사용할 것을 주장
- 이후 일관된 원자량과 분자식이 점차 발전
Mendeleev와 Meyer
- 오늘날과 매우 유사한 주기율표를 독자적으로 제안, 원자 이론 발전이 급속도로 이루짐
2.1.1 주기율표
- Mendeleev와 Meyer: 원자량에 따라 원소 나열, 비슷한 성질을 가진 원소의 무리 확인
- Mendeleev: 무리들을 가로 또는 세로로 배열하고 원자량 뿐만 아니라 화학적 행동의 유사함을 고려하여 빈칸 찾음
- 그 당시 발견되지 않았던 원소(갈륨, 스칸듐, 저마늄, 폴로늄)의 성질 예측
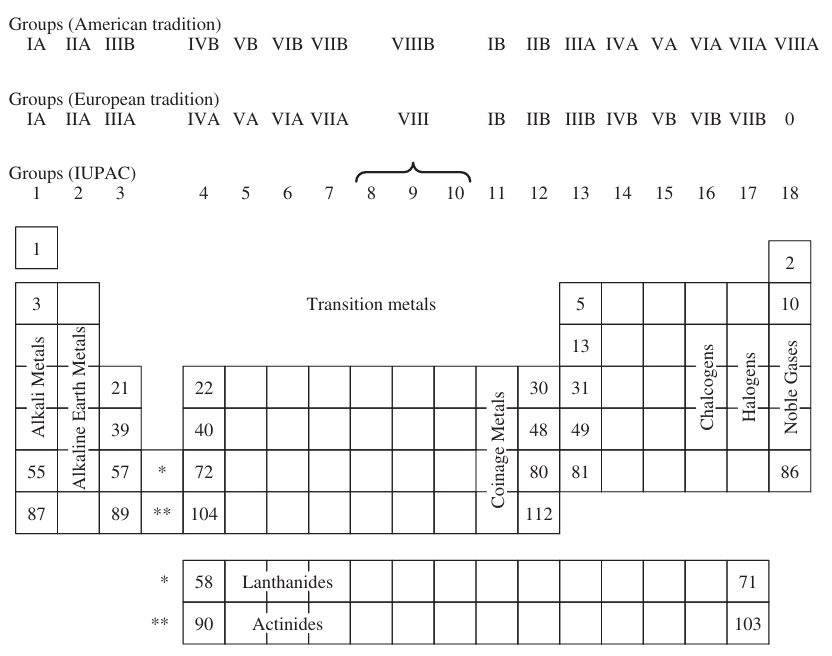
현대 주기율표
- 수평열: 주기(Period)
- 수직열: 족(group or family)
- IUPAC: 족을 1번부터 18번까지로 표시하는 것을 권장
2.1.2 원자구성 입자(Subatomic Particles)의 발견과 Bohr 원자
원자분광학
- 개개 원소가 전기 방전 또는 열에 의해 들뜰 때 특정한 에너지의 빛을 방출
- Balmer: 수소 원자가 가시광선에서 해당하는 에너지를 방출함을 보임



- 방출한 에너지 E는 빛의 파장, 진동수, 파수와 관련이 있음


- 가시광선 영역의 빛의 방출 뿐만 아니라, Balmer 식에 의해 적외선, 자외선 영역에서의 발광을 수소 원자의 스펙트럼에서 발견
- n: 양자수(quantum numbers)
- 이 에너지의 근원은 Niels Bohr의 원자에 대한 양자 이론 이후 알게됨
- 양자 이론은 1913년에 처음으로 발표, 10년에 걸쳐 다듬어짐
- 원자 내의 음으로 하전된 전자가 양으로 하전된 핵 주위를 에너지의 흡수나 방출 없이 안정한 궤도를 회전한다고 가정
- 그러나, 전자는 특정한 에너지에 해당하는 빛을 흡수하고, 높은 궤도로 들뜰 수 있음
- 전자는 또한 특정한 에너지에 해당하는 빛을 방출하고, 낮은 에너지 상태의 궤도로 떨어질 수도 있음
- 방출하거나 흡수한 빛의 에너지: 수소 원자의 Bohr 모형에 따라 다음 식으로부터 구할 수 있음

※ μ : 전자-핵 조합으로 이루어진 환산 질량
※ Z : 핵의 전하
※ e : 전자 전하
※ h : Plank 상수
※ nh : 높은 에너지 상태를 나타내는 양자수
※ nl : 낮은 에너지 상태를 나타내는 양자수
※ 4πε0: 진공에서의 유전율
- 식: Rydberg 상수가 핵의 질량뿐만 아니라 기본 상수에도 의존한다는 것

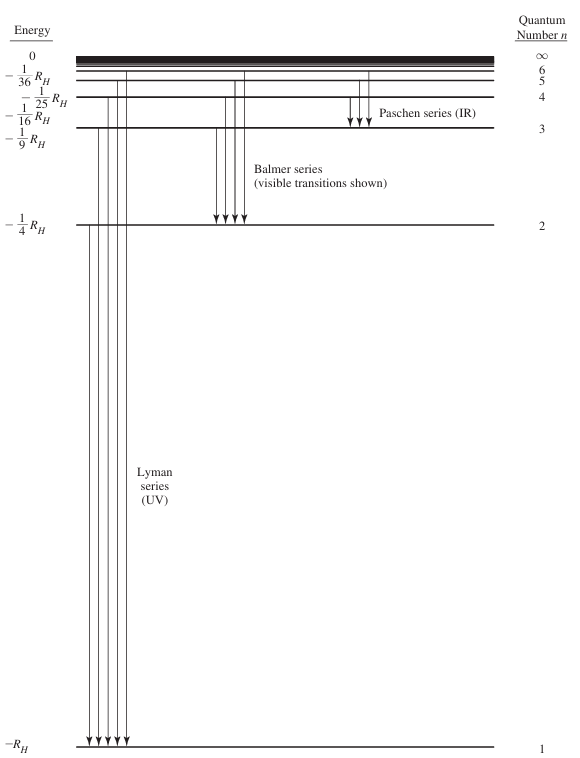
- 전자 떨어짐에 따라 에너지를 전자기 복사선의 형태로 내놓음
- 반대로, 동일한 복사선 에너지가 원자에 의해 흡수되면 전자는 nl에서 nh로 올라감
- 작은 n 값에서는 에너지 간격이 크며, 큰 n 값에서는 에너지 간격이 아주 가까워 짐
- n이 무한대에 접근 시 0의 한계에 접근
- 양자수가 무한대라는 것은 핵과 전자가 분리된 개체라는 것을 의미
기본문제 2.1
Q. 수소 원자에 대하여 nh = 3에서 nl = 2로 전이할 때 에너지를 줄과 cm-1(분광학에서 흔히 쓰이는 단위, ṽ가 E에 비례하기 때문에 에너지 단위로 자주 쓰임) 단위로 계산하라. 이 전이는 수소의 가시광선 방출 스펙트럼에서 붉은 선으로 나타난다.
(참고: RH= = 수소에 대한 Rydberg 상수 = 1.097 x 107m-1 = 2.179 x 10-18 J = 13.61 eV
풀이:
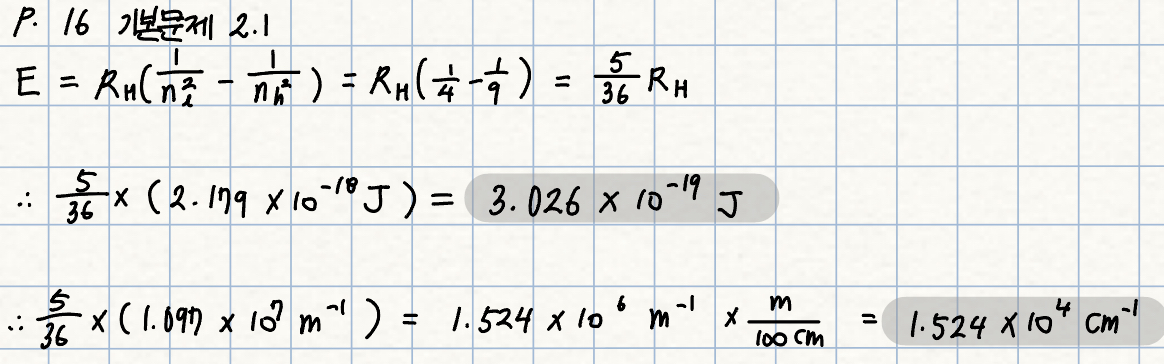
- Bohr 이론은 수소 원자에 적용할 때 잘 맞았음
- But, 2개 이상의 많은 전자를 갖고있는 원자에 적용할 경우 이 이론은 맞지 않았음
- 원형 궤도 대신 복잡한 타원형 궤도에 대한 데이터를 Bohr 이론에 맞추기 위해 도입하기도 하였으나, 성공하지 못함
- 에너지 준위는 오로지 수소 원자와 He+, Li2+, Be3+ 같이 전자가 하나인 화학종에만 적용할 수 있었으며, 전자의 중요한 특징인 파동 성질을 고려해야 할 필요성이 생긴 것
de Broglie 식
- 모든 움직이는 입자는 다음 식으로 설명되는 파동 성질을 갖고있음
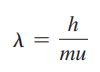
λ = 입자의 파장
h = Plank 상수
m = 입자의 질량
u = 입자의 속도
- 눈으로 볼 수 있는 정도의 큰 입자는 파장이 너무 짧아 측정이 불가능
- 반면, 전자는 질량이 매우 작아 파동성을 갖고 있음
- Bohr 이론처럼 핵 주위를 원형으로 회전하는 전자는 de Broglie 식에 따라 설명할 수 있는 정지파를 형성한다고 생각할 수 있으나,
- 원자 내 전자의 운동을 정확히 설명하는 것은 불가능
- Heisenberg의 불확정성 원리(Heisenberg's uncertainty principle)
- 전자의 위치와 운동량의 본질적인 불확정성 관계가 존재한다는 것
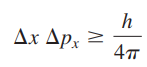
- △x = 전자 위치의 불확정성
- △px = 전자 운동량의 불확정성
- 원자 내 전자의 정확한 에너지 결정 가능, 즉 정확한 운동량(작은 △px) 측정 가능
- 즉, Heisenberg의 원리에 따르면 전자의 위치에 큰 불확정성이 있음(큰 △x)
- 전자의 운동을 정확히 설명할 수 있는 단순한 입자로 취급할 수 없음
- 위치에 대한 불확정성을 가진 파동성의 전자로 취급해야 함
- Bohr 이론에 따라 전자의 정확한 궤도(orbit)를 설명하기보다 전자를 발견 가능한 궤도함수(orbital)로 설명
- 공간상의 특정한 곳에서 전자를 발견할 수 있는 확률(probability, 전자밀도(electron density))은 원리상 계산 가능
Keyword: 주기(period), 족(group, family), 양자수(quantum numbers), 주양자수(principal quantum numbers), Heisenberg의 불확정성 원리(Heisenberg's uncertainty principle), 궤도(orbit), 궤도함수(orbital), 확률(probability), 전자밀도(electron density)



