고등학교 2학년 때 과학 수업 실연대회에 참가하기 위해 준비했던 자료들!
친구와 2인 1팀으로 금상 수상했다
지금 보면 간단간단하지만, 저 당시 이 대회를 기획하고 자료 만들고 발표 준비하느라 몇날 며칠을 고생했던 기억이 ㅎㅎ
자료를 찾아보니까 그 당시 초등임용 수업 실연 시나리오 자료도 찾아보면서 반영하고 고생 많았네
좋은 결과가 있어서 다행이었다
과학 수학 수업 실연 대회 참가 양식
과목: 수학+과학
주제: 세상에서 가장 아름다운 수식, 오일러 공식
학습 목표: 파동과 삼각함수와의 관계를 알아보고, 오일러 공식에 대해 알 수 있다.
수업 형태: 강의식 및 탐구식 수업
도입(5분):
<자연계의 파동 모양과 삼각 함수 그래프의 연관성 인식> : y=sin x 의 그래프와 y= cos x의 그래프는 파동의 모양을 하고 있으며, 자연계의 음파나 빛의 파동과 비슷한 모양임을 그래프로 직접 확인해본다.
전개(40분):
<자연계의 파동에 대한 설명> - 3분 : 앞서 도입부분에서 이야기 했던 대표적인 예로, 음파와 빛의 파동에 대해 설명한다.
→음파와 빛의 파동에 대한 그래프를 그려본 뒤, 자연계의 파동은 삼각함수를 이용해 나타낼 수 있다는 것을 상기시킨다.
< π, i, e 는 서로 관계가 있을까?> - 7분
: π는 원에서 생긴 수, i는 방정식의 해를 구하기 위해 생긴 수, e는 돈 계산에서 생겼다는 수 이다. 얼핏 보면 서로 관련이 없어보이는 이 세 수가 어떤 관련성을 가지고 있는지 함께 탐구해 보는 시간을 가진다.
<테일러 전개를 이용한 지수함수와 삼각 함수의 대 변신!> - 15분
: 지수 함수와 삼각 함수가 정수만 사용한 다항식으로 나타낼 수 있음을 알아낸다. 어떤 함수를 항의 수가 무한히 계속되는 다항식으로 나타내는 것을 ‘테일러 전개’라고 한다.
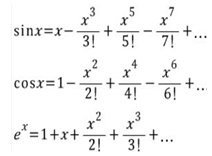
<삼각 함수와 지수 함수를 연결하는 연결 다리, 허수!> - 15분
: 제곱하면 음수가 되는 불가사의한 수, 허수를 이용하여 오일러 공식을 완성해 낼 수 있다. 지수함수의 x에 ix를 대입한다. e(ix)란 e를 허수 제곱하는 것을 의미한다.
계산을 이어나가면, 실수부는 cos x와 같아지고, 허수부는 sinx와 같아진다. 이리하여, 오일러 공식이 새롭게 완성된다.
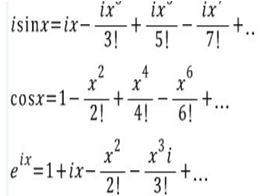

정리(5분)
: 수학의 기본을 이루는 1,0,e,π 및 허수 I로 이루어 져 있는 오일러의 식의 아름다움에 대해 깨닫게 한다. 허수의 지수함수 e(ix) 의 값은 복소수가 되며, 가우스의 평면 위에서 회전함을 알게 한다. 마지막 정리 퀴즈를 통해 수업을 마무리한다.
발표 파워포인트
당시에도 유행했던 자까님의 대학일기 캐릭터 PPT
출처는 혜링이 블로그이다
수업 실연이다보니 실제로 발표를 들으시는 분들은 학교 선생님들이었지만
학생으로 가정하고 이목을 끌기 위해 재밌는 PPT 양식을 사용하였다



여기에 두 물체가 있습니다. 하나는 소리굽쇠이고, 다른 하나는 촛불인데요, 먼저 소리굽쇠는 악기의 조율 등에 사용되는 , 끝이 U자 모양을 한 금속제 도구입니다. 두들기면 U자 모양의 부분이 항상 같은 진동수로 진동하여 일정한 높이의 소리를 냅니다. 소리굽쇠의 진동은 공기를 진동시켜 음파가 됩니다. 여기서 마루에서 마루, 또는 골에서 골의 거리를 파장이라고 하고, 파동의 마루의 높이, 또는 골의 높이를 진폭이라고 합니다. 두번째로 빛의 파동이란, 전기장과 자기장의 진동이 파동이 되어 공간이나 물질 속을 퍼져나가는 현상입니다. 전기를 띤 입자가 진동하면 전자기파가 발생하는 것입니다. 우리가 볼 수 있는 ‘가시광선'은 파장이 약 380~780nm 인 전자기파 입니다.

여기서 잠깐! 이 두 자연계의 파동이, 수학시간에 배운 어떤 함수의 형태와 유사하지 않나요?

네. 바로 삼각함수인 sin과 cos 그래프입니다. 사인과 코사인 그래프는 파동의 모양을 하고 있으며, 자연계의 음파나 빛의 파동 등과 비슷한 모양입니다. 뒤에서 자세히 배울 오일러 공식에 사용되는 삼각함수 입니다. 오일러 공식이나 오일러 등식은 물리학에서 매우 소중히 여기는 편리한 식인데요, 그 배경에는 ‘자연계의 파동은 삼각함수를 이용해 나타낼 수 있다' 라는 사실이 있습니다.

본격적으로 배울 오일러 함수는, 많은 과학자와 수학자 다수가 ‘세계에서 가장 아름다운 식'이라고 부른다고 합니다. 저는 처음에 왜 이게 아름다운 식이지? 라고 하며 이해가 잘 안갔는데요, 위의 식에서 볼 수 있다싶이, 네이피어 수 e, 허수 단위 I, 원주율 파이 는 각각 태생이 서로 다른, 본래 아무 관련도 없다고 생각되는 수입니다. 그런데도 e와 i와 파이 를 e(ix) 라는 형태로 정리하고, 1을 더하면 놀랍게도 0이 된다는 사실에 많은 수학자와 과학자들이 신비적인 감정조차 느꼈다고 합니다. 이렇듯 세가지의 서로 다른 수가 하나의 식으로 표현될 수 있다는 것은 굉장히 놀라운 것이라 볼 수 있습니다.
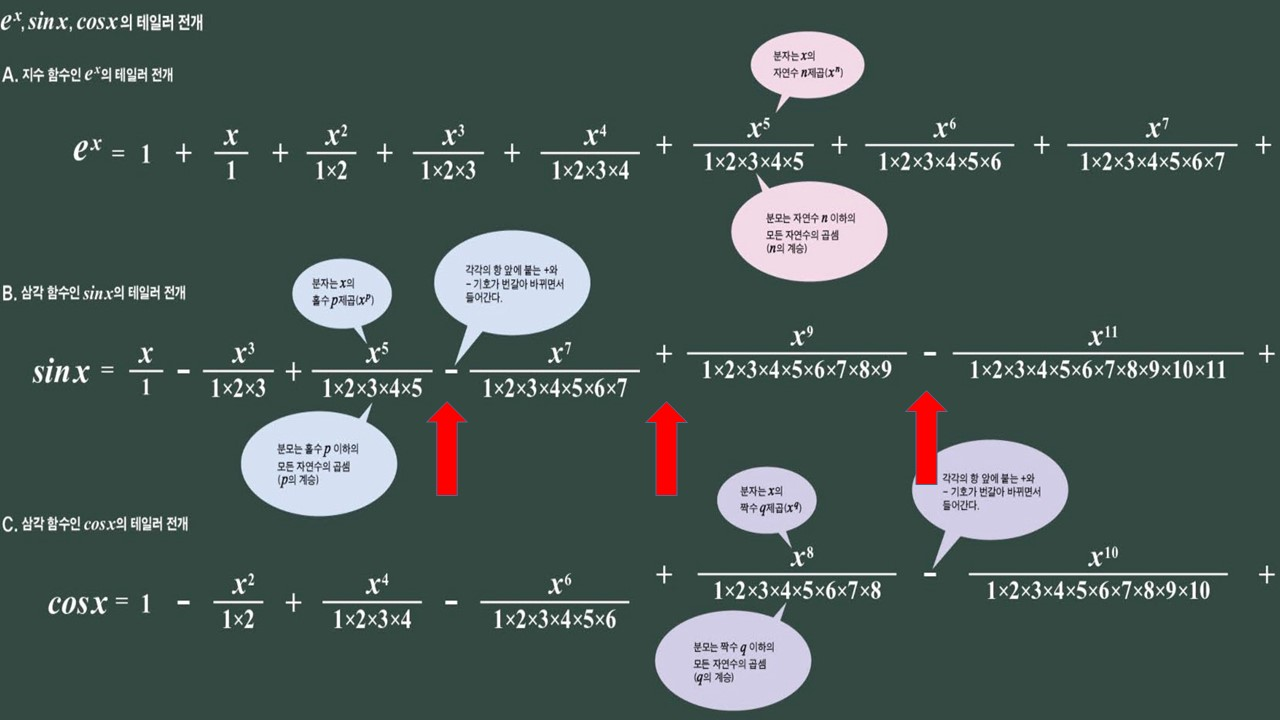
지수 함수인 e(x)와, 삼각 함수인 sinx, cosx 등의 함수는,보시다 시피 x와 그 거듭제곱과 정수만 사용한 다항식으로 나타낼 수 있습니다. 단, 간단한 다항식이 아니라 위에 나타난 것처럼 항의 수가 무한히 계속되는 다항식 인것입니다. 이처럼 어떤 함수를 항의 수가 무한히 계속되는 다항식으로 나타내는 것을 ‘테일러 전개'라고 합니다. 위의 다항식은 테일러 전개의 특수한 경우로, 매클로린 전개라고도 합니다. 자, 이 식들을 볼때, 이제는 e(x) 와 sin, cos 그래프가 비슷하다고 느껴지지 않나요? 이 세개의 식은 정수를 사용해 유사하고, 매우 규칙적으로 모양을 띤다는 것을 알 수 있습니다.
자세히 들여다보면,
sin x를 테일러 전개한 식은 e(x)를 테일러 전개 한 식과 비슷하지만, x의 홀수 제곱항만으로 되어있으며, x의 짝수 제곱항이 없습니다. 그리고 각각의 항 앞에 붙는 +와 –기호가 번갈아 바뀌면서 들어가 있습니다. 한편 cos 그래프를 테일러 전개한 식은 1과 x의 짝수 제곱항만으로 되어 있으며, x의 홀수 제곱항이 없다는 것을 알 수 있습니다. 각각의 항 앞에 붙는 +와 – 기호가 번갈아 바뀌면서 들어간 것은 sin x 의 경우와 같죠. 단순히 ex와 sinx, cosx 를 알았을 때는 그저 신기하기만 했었는데, 이렇게 세 수가 굉장히 규칙적이고, 아름다운 식으로 나타낼수 있음에 참 놀라웠습니다.

자, 이제 오일러 식을 유도할 수 있는데요, 먼저 e(x)를 테일러 전개한 식에 x=ix를 대입합니다. 그리고, 1과 x의 짝수 제곱항과, x의 홀수 제곱항으로 나누어 봅니다. Sin x를 테일러 전개한 식과 cos x를 테일러 전개한 식을 이용하면, e(ix)= cos x + i sin x 를 유도할 수 있는 것입니다. 마지막으로, 오일러의 공식에 x= 파이 를 대입해 봅니다. Cos 파이= -1, sin 파이 = 0 이므로, 여기서 오일러 등식을 유도할 수 있게 되는 것 입니다. 삼각 함수는 본래 다루기가 까다로운 함수입니다. 예를 들어 sin x를 미분하면 cos x로 바뀌고, cos x 를 미분하면 –sin x로 바뀌어서 계산이 복잡하게 됩니다. 하지만, 지수함수는 다루기가 간편합니다. 예를 들어 y= e(x)를 미분해도 y=e(x)로 변하지 않는 것이죠. 이 때문에 삼각함수의 계산 대신에 오일러 공식을 이용해서 지수 함수로 계산하면 문제가 간단해지는 경우가 많이 있습니다. 이 때문에 오일러 공식이 수학자나 물리학자들에게 매우 소중하게 받아들여지는 주된 이유입니다.

마지막으로 퀴즈 타임을 가지고 마무리 하겠습니다.

발표 PPT 파일
다시 고등학교 시절로 돌아가고 싶다 ㅠㅠ