2.1 원자 이론의 역사적 발전
2.1.1 주기율표
2.1.2 원자구성 입자(Subatomic Particles)의 발견과 Bohr 원자
2.2 Schrodinger 방정식
2.2.1 상자 속 입자(Particle in a Box)
2.2.2 양자수와 원자 파동함수
2.2.3 쌓음 원리
2.2.4 가려막기
2.3 원자의 주기적 성질
2.3.1 이온화 에너지
2.3.2 전자 친화도
2.3.3. 공유 반지름과 이온 반지름
2.2 Schrodinger 방정식(2)
2.2.2 양자수와 원자 파동함수
- 상자 속 입자의 예 : 일차원에서 파동함수가 어떻게 작용하는가를 보여줌
- 수학적으로 원자 궤도함수는 삼차원 Schrödinger 방정식의 각각의 해
- 일차원 상자에서 사용한 동일한 방법을 삼차원 원자에 대해 확장
- 이 궤도함수 식은 3개의 양자수, 즉 n, l, ml을 포함하고 있음
- 네 번째 양자수인 ms는 Schrödinger 방정식에 대한 상대론적 수정의 결과물, 전자의 자기모멘트를 설명함으로써 완성됨

- n(주양자수): 원자 궤도함수의 주요 에너지 부분을 결정
- l(각운동량 양자수): 궤도함수의 각운동량 또는 궤도함수의 모양을 결정, 궤도함수의 에너지에 작은 영향을 미침
- ml(자기 양자수): 자기장하에서 각운동량 벡터 또는 공간에서 궤도함수의 위치 결정
- ms(스핀 양자수): 자기장 하에서 전자 자기모멘트의 배향 결정, 자기장과 같은 방향(1/2), 다른 방향(-1/2)
- 장이 존재하지 않는 경우 모든 ml 값 (3개의 p 궤도함수 또는 5개의 d 궤도함수)은 같은 에너지를 갖게 됨
- 2개의 ms 값 또한 같은 에너지를 갖게 됨
- 양자수 ms : 원자 내 전자스핀을 나타냄
- 최외각 전자 1개를 지닌 알칼리 금속 원자의 빔이 자기장을 지나갈 때 두 부분으로 나누어진다는 것
- 한 부분의 알칼리 금속 빔은 자극으로 끌리고, 다른 부분의 알칼리 금속 빔은 다른 쪽 자극으로 끌림
- 고전물리에서 전하를 띤 입자가 회전할 때 자기모멘트(전자를 작은 자석으로 생각)를 생성하여 자기장의 백터 방향과 스핀 방향(시곗바늘회전방향 또는 반대 방향)이 연관 관계를 가지게 됨
- 전자의 스핀처럼 묘사할 수 있으나, 이는 어디까지나 양자역학적인 성질이며, 전자를 고전역학에 적용하는 것은 부정확한 일

- p 궤도함수와 d 궤도함수 파동방정식에서 i가 나타나는 것
- 복소함수보다는 실함수를 사용하는 것이 훨씬 편하기 때문에 종종 파동방정식의 다른 성질을 이용함
- 미분방정식에 대해 방정식 해의 선형결합(함수의 합 또는 차, 각각에 대하여 특정한 계수를 곱함) 또한 방정식의 해임
- p 궤도함수에 대해 선택하는 조합은 ml = +1과 -1을 갖고 있는 p 궤도함수의 합과 차이며, 1/루트 2과 i/루트 2를 곱하여 정규화함

- 같은 과정을 ml = ±1과 ml = ±2를 가진 d 궤도함수에 사용하면 표 2.3의 θØ( θ, Ø)로 시작하는 칸에 있는 함수 얻게 됨
- 이는 d 궤도함수임
- dz2 궤도함수(ml = 0)는 실제로 2z2 - x2 - y2 함수를 이용하는데, 편의상 z2라고 사용
- 이 함수들은 실함수임
- 따라서 ψ = ψ*이고, ψ ψ* = ψ2임
- Schrödinger 방정식을 자세히 살펴보면 원자 궤도함수의 수학적 유래를 알 수 있음
- 삼차원에서 ψ는 Cartesian 좌표(x, y, z) 또는 구좌표(r, θ, Ø)로 표현할 수 있음
- 구좌표 : r 값이 핵으로부터의 거리를 나타낼 때 유용
- 구좌표에서 θ는 z 축으로부터의 각도로서 0부터 π까지 변화하며, Ø는 x축으로부터의 각도로서 0부터 2π까지 변화
- Cartesian 좌표와 구좌표는 아래 방정식을 사용하여 서로 변환 가능

- 구좌표에서 부피 요소의 세 면은 r dθ, r sinθ d Ø, dr
- 세 면의 곱은 r2 sinθ dθ dØ dr이며, dx dy dz와 같음
- r과 r + dr 사이의 얇은 껍질에 대한 부피는 4πr2 dr이며, Ø에 대하여 0부터 π, θ에 대하여 0부터 2π 까지 적분한 값
- 이 적분은 핵으로부터 거리의 함수로서 전자밀도를 표현하는 데 유용
- ψ는 방사방향 성분과 각 성분으로 분해할 수 있음
- 방사방향 함수(radial function) R : 핵으로부터 서로 다른 거리에서의 전자밀도를 나타냄
- 각운동량 함수(angular function) : θ와 Ø는 궤도함수의 모양과 궤도함수의 공간상 배향을 나타냄
- 두 가지 각 인자는 Y라고 부르는 하나의 인자로 묶기도 함

- R은 오직 r의 함수임
- Y는 θ와 Ø의 함수이며, s, p, d와 다른 궤도함수의 특징적인 모양을 알려줌
각운동량 함수
- 각운동량 함수 θ와 Ø는 원자 중심으로부터 주어진 거리에서 한 지점으로부터 다른 지점까지 확률이 어떻게 변화하는가를 결정함
- 이는 궤도함수의 모양과 공간상의 배향을 알려줌
- 각운동량 함수 θ , Ø는 양자수 l, ml에 의하여 결정됨
- s, p, d 궤도함수의 모양은 다음과 같음

방사방향 함수
- 방사방향 인자 R(r)는 각운동량 양자수 l에 의하여 결정됨
- 방사방향 확률함수(radial probability function)는 4 π r2 R2임
- 이 함수는 모든 각도에 걸쳐 적분한 결과인 4 π r2을 갖고있음
- n = 1, 2, 3에 해당하는 궤도함수에 대하여 방사방향 파동함수와 방사방향 확률함수 도시
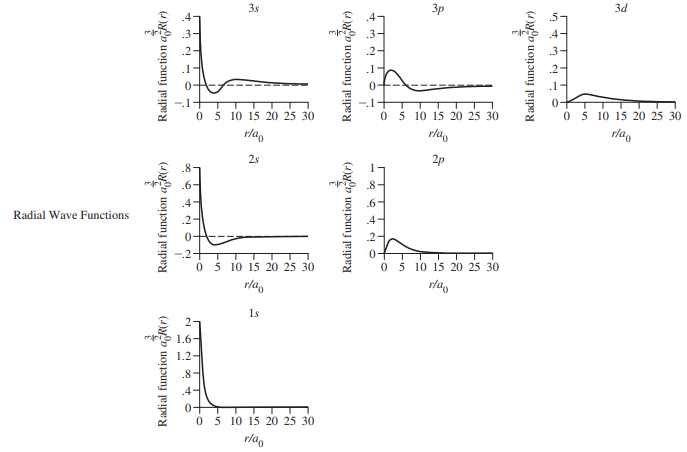
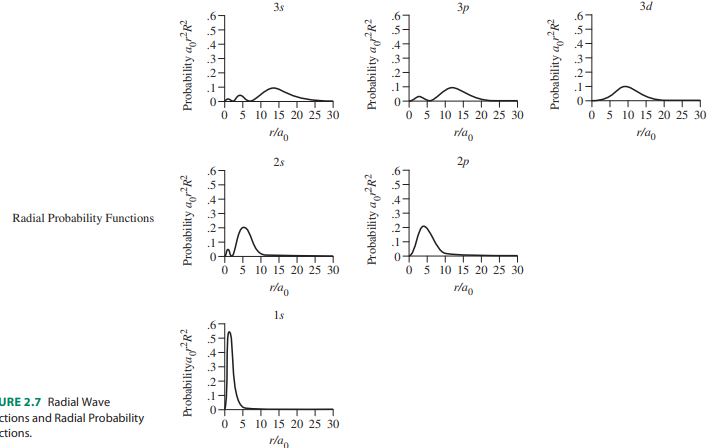
- R(r)과 4 π r2 R2은 Bohr 반지름 a0 비율로 나타나 있으며, a0는 그래프의 축 단위로 적절
- Bohr 반지름인 a0 = 52.9 pm는 양자역학에서 흔히 사용하는 단위
- 이는 수소 1s 궤도함수에 대해 ψ2 값이 최대치일 때의 r 값이며, Bohr 모형에 따른 n = 1일 때의 반지름임
- 모든 방사방향 확률 도표에서 전자밀도 또는 전자를 발견할 확률은 핵으로부터의 거리가 증가할수록 급격히 떨어짐
- 1s 궤도함수에서 가장 빨리 떨어지며, r = 5a0에서 확률은 0에 접근함
- 반면 3d 궤도함수는 r = 9a0에서 최대치를 보이며, r = 2a0에 이르기까지 0에 접근하지 않음
- s 궤도함수를 포함한 모든 궤도함수는 핵 중심에서 그 확률이 0임 (r일 때 4 π r2 R2 = 0이기 때문)
- 방사방향 확률함수는 r 값에 따라 급격히 증가하는 4 π r2과 R2의 조합으로 이루어져 있으며, 최대치와 최소치를 가질 수 있음
- 그러나, 일반적으로 r 값에 따라 지수함수도 감소함
- 두 인자의 곱은 특유의 확률을 나타냄
- 화학반응은 핵으로부터 먼 거리에서 궤도함수의 모양과 크기에 영향을 받으므로 방사방향 확률함수는 어느 궤도함수가 화학반응에 참여할 것인지에 도움을 줌
마디 표면
- 핵으로부터 먼 거리에서 전자밀도 또는 전자를 발견할 수 있는 확률은 급격히 떨어짐
- 2s 궤도함수 또한 표면에서 전자밀도가 0인 마디 표면(nodal surface)를 갖는데, 이 경우 r = 2a0인 구에서 확률이 0임
- 마디는 전자의 파동성의 결과로 자연히 나타나는데, ψ에 대한 파동방정식을 푼 결과 함수에서 나타남
- 마디는 파동함수의 부호가 바뀔 때(2s 궤도함수의 r = 2a0에서) 0이 되는 표면임)
- 이는 ψ = 0이 되는 것을 요하며, 그 표면에서 전자를 발견할 확률은 0임
- 만약 전자를 발견할 확률이 0이면( ψ2 = 0 ), ψ도 반드시 0이어야 함
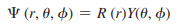
이므로, ψ = 0이 되기 위해서는 R(r) = 0 또는 Y( θ, Ø ) = 0이어야 함
- 따라서, 어떤 조건에서 R(r) = 0 또는 Y( θ, Ø ) = 0이 되는지를 결정함으로써 마디 표면을 결정할 수 있음
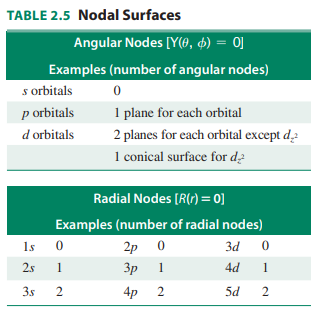
- 몇몇 d나 f 궤도함수의 원뿔 모양 마디를 2개로 계산할 경우 특정한 궤도함수의 전체 마디수는 n-1 개임
- 각운동량 마디(angular nodes)는 Y = 0이고 평면 또는 원뿔 모양에서 나타남
- 각운동량 마디는 θ와 Ø에 의하여 결정될 수 있음
- 그러나 Y를 Cartesian 좌표(x, y, z)로 표현하면 보기가 쉬움
- 파동함수가 양의 영역인지, 어디가 음의 영역인지 알 수 있음
- 어떠한 궤도함수도 l개의 각운동량 마디가 있으며, dz2 궤도함수와 유사한 궤도함수의 원뿔 표면은 2개의 마디로 취급
- 방사방향 마디(radial nodes) 또는 구형 마디(spherical nodes)
: R = 0일 때 나타나며, 3s와 3pz 궤도함수에 대해 원자가 층으로 이루어진 것처럼 보이게 함
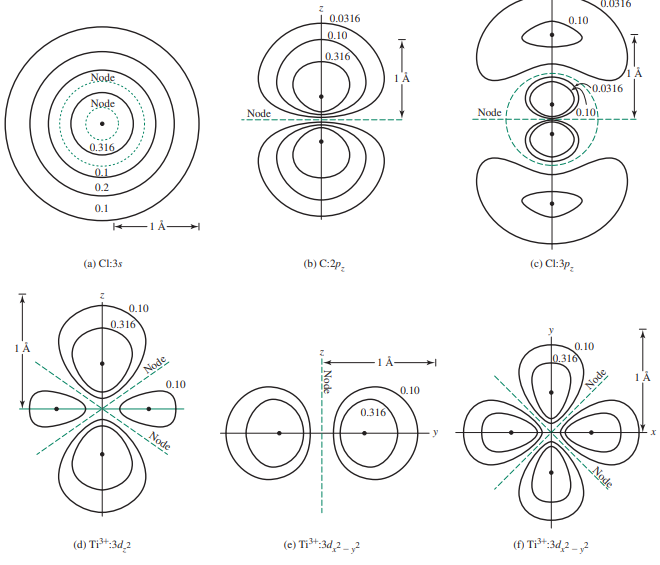
- 이 마디는 방사방향 함수의 부호가 바뀔 때 나타남
- 이는 R(r) = 0에 대하여 방사방향 함수 그래프로 그리고 4 π r2과 R2 = 0에 의하여 방사방향 확률 그래프로 나타낼 수 있음
- 1s, 2p, 3d, 4f 및 기타 궤도함수(각각의 모양에서 가장 낮은 에너지 궤도함수)는 방사방향 마디가 없고, n 값이 증가함에 따라 방사방향 마디수는 증가
- 주어진 궤도함수에 대해 방사방향 마디수는 항상 n-l-1임
- 마디 표면은 당혹스럽게 할 수 있음
- 그 예로, p 궤도함수는 핵을 통과하는 마디면을 갖고있음
- 어떻게 전자가 확률이 0인 마디에서 존재하지도 않고 마디의 양쪽에서 동시에 나타날 수 있나?
- 상대적인 관점에서 확률이 확실히 0까지 가지 않는다는 것
- 이와 같은 질문은 전자를 파동으로 생각할 때 실제로 아무런 의미가 없음
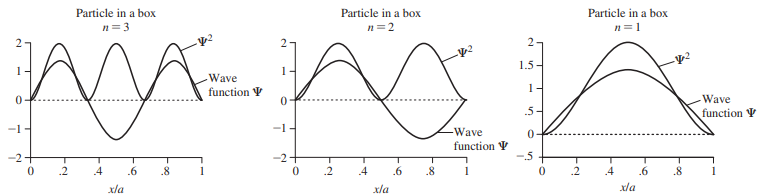
- n = 2에 대하여 x/a = 0.5, n =3에 대하여 x/a = 0.33 및 0.67에서 마디를 보여줌
- 같은 그림으로 기본 진동수(n = 1)와 그 배수인 n = 2와 3에서 진동하는 줄의 진폭을 나타낼 수 있음
- 잡아당긴 바이올린 줄은 특정 진동수에서 진동, 진폭이 0이 되는 곳에 있는 마디가 생기는 것은 자연스러운 결과
- 진폭이 0이라는 것은 그 지점에 줄이 존재하지 않는 다는 것은 아님
- 단순히 진동의 크기가 0이라는 것
- 바이올린 줄이 진폭이 0인 양쪽지점에도 존재하는 것처럼 전자 파동은 마디뿐만 아니라 마디 표면의 양쪽에도 존재
예제문제 2.1
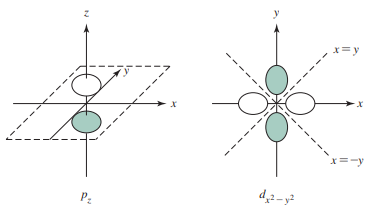
- pz 마디 구조 각운동량 인자 Y는 Cartesian 좌표로 표 2.3에 있음
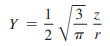
- 이 궤도함수는 z가 Y 표현에 있기 때문에 pz라고 나타냄
- 각운동량 마디에 대하여 Y는 0이어야 하며, 오로지 z = 0일 경우에만 그러함
- z = 0 (xy면)은 pz 궤도함수에 대한 각운동량 마디 표면임
- 파동함수는 z > 0인 곳에서 양의 값을 갖고, z<0인 곳에서 음의 값을 가짐
- 2pz 궤도함수는 방사방향(구형) 마디가 없고, 3pz 궤도함수는 하나의 방사방향 마디를 갖고 있으며, 그 다음은 같은 방식을 따름
- d x2-y2의 마디 구조
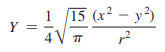
- Y = 0인 방정식에 대해 해가 2개이므로 이 방정식에 의해 정의된 면은 각운동량 마디 표면임
- 이는 z축을 포함하고 x와 y축에 대해 45도 각도를 이루는 면임
- 함수는 x > y인 곳에서 양이고, x < y인 곳에서 음임
- 따라서 3 d x2 - y2 궤도함수는 방사방향 마디가 없고, 4 d x2-y2는 하나의 방사방향 마디를 갖고있으며, 그 다음도 같은 방식을 따름
기본문제 2.2
Q. 각 파동함수가 다음과 같은 d z2 궤도함수에 대하여 각운동량 마디 표면을 나타내라.
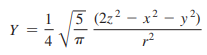
기본문제 2.3
Q. 각 파동함수가 다음과 같은 dxz 궤도함수에 대하여 각운동량 마디 표면을 나타내라
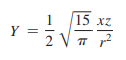
풀이:
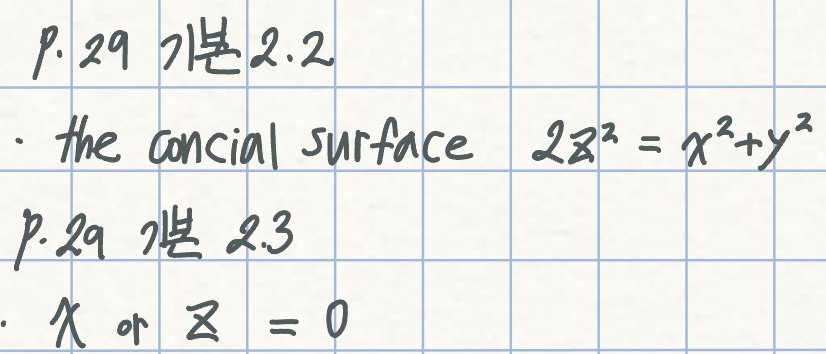
Keyword: 방사방향 함수(radian function), 각운동량 함수(angular function), 방사방향 확률함수(radial probability function), 마디 표면(nodal surface), 각운동량 마디(angular nodes), 방사방향 마디(radial nodes), 구형 마디(spherical nodes)



